Autarquia Educacional de Afogados da Ingazeira - AEDAI
Faculdade de Formação de Professores de Afogados da Ingazeira - FAFOPAI
Departamento de matemática
Disciplina: Álgebra Linear
Professora: Eliana Nogueira
Aluno: Edson Marcos Silvestre Campos
E-mail: emarlg@hotmail.com
A ALGEBRA LINEAR / TRANSFORMAÇÕES LINEARES: UMA GRANDE PARCERIA
Atualmente, a matemática é distribuída de forma pronta e acabada, sendo ela melhor compreendida quando é explorada devidamente, alem de seu histórico ser o maior aliado para o seu entendimento. Todos os conhecimentos que hoje adquirimos na matemática básica ou complementar tiveram inicio na babilônia por volta do século IX e VIII a.C. Nesta época, os egípcios e babilônios já desenvolviam a álgebra no seu cotidiano, de acordo com suas necessidades, por meio de sistemas aritméticos avançados, facilitando a resolução de problemas que surgiam no seu cotidiano, e que hoje seriam resolvidos por meio de equações lineares, equações quadráticas e equações indeterminadas. Em outros casos esses sistemas aritméticos eram resolvidos através de equações geométricas, desenvolvidas pelos seguintes matemáticos: Papiro Rhind, Sulba Sutras e elementos de Euclides.
A álgebra tem como objetivo estudar as generalizações dos conceitos e operações de aritmética. Esse termo foi desenvolvido pelo seu pai e possíveis seguidores: Al – Khawarizmi (780-850), François Viète (1540-1603) e Diofante (250-350), respectivamente. Com base nesse contexto podemos dizer que a álgebra linear é um avanço continuo da álgebra, pelo qual estuda-se equação de sistemas lineares algébricos ou diferenciais e que se utiliza alguns fatores como: vetores, espaços, subespaços, matrizes e entre outros que contribuem para a sua resolução enquanto álgebra.
Através deste histórico podemos dizer que algumas funções ordinais como: a função f definida pela equação f(x) = x2, transformam um número real em outro número real, no caso, no seu quadrado. Por exemplo, o número 2 é transformado em 4, isto é, f(2) = 4. Com isso podemos observar que as os tipos especiais de função transformam vetores em outros vetores, preservando assim as operações de adição vetorial e multiplicação por escalar, podendo ser chamada também de Aplicação linear ou mapa linear nos casos em que o domínio e contradomínio coincidem é usada à expressão Operador Linear.
Exemplo: Lembramos que uma função f de um conjunto A em um conjunto B, f : A em B, é uma regra que associa a cada elemento do conjunto A, um único elemento do conjunto B. O conjunto A é chamado domínio e o conjunto B é chamado contradomínio. O subconjunto de B formado pelos elementos b pertencente à B tais que f (a) = b, para algum a pertencente à A é chamado (conjunto) imagem de f . Para todo elemento a pertencente à A, f (a) é chamado a imagem de a por f . Dizemos também que f leva a em f (a). Através deste e de outros exemplos, podemos definir a transformação linear com as seguintes propriedades:
Exemplo: Lembramos que uma função f de um conjunto A em um conjunto B, f : A em B, é uma regra que associa a cada elemento do conjunto A, um único elemento do conjunto B. O conjunto A é chamado domínio e o conjunto B é chamado contradomínio. O subconjunto de B formado pelos elementos b pertencente à B tais que f (a) = b, para algum a pertencente à A é chamado (conjunto) imagem de f . Para todo elemento a pertencente à A, f (a) é chamado a imagem de a por f . Dizemos também que f leva a em f (a). Através deste e de outros exemplos, podemos definir a transformação linear com as seguintes propriedades:
Sejam V e W espaços vetoriais sobre o mesmo corpo K.
Diz-se que uma função T de V em W é uma transformação linear se
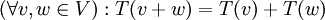 ;
;
 . Exemplos de transformações lineares:
. Exemplos de transformações lineares:
a função T de K em K definida por T(x) = 3x;
a função T de K2 em K definida por T(x,y) = x + y;
a função T de K2 em K2 definida por T(x,y) = (3x + y,2x − 2y);
se D for o espaço das funções deriváveis de R em R e se F for o espaço de todas as funções de R em R, então a derivação (isto é, a função de D em C que envia cada função na sua derivada) é linear. Em contrapartida, se a = K \ {0}, então a função T de K em K definida por T(x) = x + a não é uma transformação linear.
Se T for uma função de um espaço vetorial V num espaço vetorial W, então afirmar que T é linear equivale a afirmar que T preserva combinações lineares de pares de vetores, isto é, para quaisquer dois vetores v1,v2 = V e dois escalares α1,α2 = K:
T(0) = 0, pois T(0) = T(0 − 0) = T(0) − T(0) = 0.
se v = V, então T( − v) = − T(v), pois T(v) + T( − v) = T(v − v) = T(0) = 0.
Com isso podemos concluir que álgebra tem um papel importantíssimo para a matemática e para as transformações lineares, facilitando a resolução de situações do nosso cotidiano. Alem disso, a álgebra passou por diversos momentos e transformações para almejar o que hoje é estudado e compreendido na matemática, com uma vasta significação e aplicação para as necessidades humanas. Com base neste breve e amplo contexto sobre a álgebra finalizo com a seguinte frase: “Complicar aquilo que é simples é lugar-comum; tornar simples o que é complicado é criatividade.” (Charles Mings - Músico americano), ou seja, ninguém tem a coragem que todos esses “loucos” pela matemática tiveram de tornar uma coisa complexa em uma coisa tão simples que utilizamos freqüentemente no nosso cotidiano. Espero que continue a surgir pessoas corajosas como estas que buscam o fácil e pratico pra toda a humanidade.
REFERENCIAS BIBLIOGRÁFICAS
• http://www.ime.unicamp.br/~hlopes/gaalt00.pdf
• http://www.ead.ftc.br/portal/upload/mat/4p/04-AlgebraLinear.pdf
• http://www.ceset.unicamp.br/~telmag/ST%20362/aula_ga_transf_linear.doc
• http://www.mat.ufmg.br/~regi/gaalt/gaalt2.pdf
• http://pt.wikipedia.org/wiki/%C3%81lgebra_linear
• http://pt.wikipedia.org/wiki/Transforma%C3%A7%C3%A3o_linear
• http://pt.wikipedia.org/wiki/%C3%81lgebra_linear
Diz-se que uma função T de V em W é uma transformação linear se
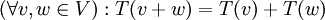 ;
; . Exemplos de transformações lineares:
. Exemplos de transformações lineares:a função T de K em K definida por T(x) = 3x;
a função T de K2 em K definida por T(x,y) = x + y;
a função T de K2 em K2 definida por T(x,y) = (3x + y,2x − 2y);
se D for o espaço das funções deriváveis de R em R e se F for o espaço de todas as funções de R em R, então a derivação (isto é, a função de D em C que envia cada função na sua derivada) é linear. Em contrapartida, se a = K \ {0}, então a função T de K em K definida por T(x) = x + a não é uma transformação linear.
Se T for uma função de um espaço vetorial V num espaço vetorial W, então afirmar que T é linear equivale a afirmar que T preserva combinações lineares de pares de vetores, isto é, para quaisquer dois vetores v1,v2 = V e dois escalares α1,α2 = K:
- T(α1v1 + α2v2) = α1T(v1) + α2T(v2)
T(0) = 0, pois T(0) = T(0 − 0) = T(0) − T(0) = 0.
se v = V, então T( − v) = − T(v), pois T(v) + T( − v) = T(v − v) = T(0) = 0.
Com isso podemos concluir que álgebra tem um papel importantíssimo para a matemática e para as transformações lineares, facilitando a resolução de situações do nosso cotidiano. Alem disso, a álgebra passou por diversos momentos e transformações para almejar o que hoje é estudado e compreendido na matemática, com uma vasta significação e aplicação para as necessidades humanas. Com base neste breve e amplo contexto sobre a álgebra finalizo com a seguinte frase: “Complicar aquilo que é simples é lugar-comum; tornar simples o que é complicado é criatividade.” (Charles Mings - Músico americano), ou seja, ninguém tem a coragem que todos esses “loucos” pela matemática tiveram de tornar uma coisa complexa em uma coisa tão simples que utilizamos freqüentemente no nosso cotidiano. Espero que continue a surgir pessoas corajosas como estas que buscam o fácil e pratico pra toda a humanidade.
REFERENCIAS BIBLIOGRÁFICAS
• http://www.ime.unicamp.br/~hlopes/gaalt00.pdf
• http://www.ead.ftc.br/portal/upload/mat/4p/04-AlgebraLinear.pdf
• http://www.ceset.unicamp.br/~telmag/ST%20362/aula_ga_transf_linear.doc
• http://www.mat.ufmg.br/~regi/gaalt/gaalt2.pdf
• http://pt.wikipedia.org/wiki/%C3%81lgebra_linear
• http://pt.wikipedia.org/wiki/Transforma%C3%A7%C3%A3o_linear
• http://pt.wikipedia.org/wiki/%C3%81lgebra_linear

Nenhum comentário:
Postar um comentário